Envy-free cake-cutting shows that resources can be split so everyone thinks they got the best cut. The simple divide and choose method works for two people, while the Selfridge-Conway procedure can be generalized to N people.
Article: The Envy-Free Cake-Cutting Procedure
Imagine you and your sibling are splitting a cake, and both of you want the best slice possible because the cake is so famously good. How should you two divide the cake fairly?
In the context of game theory, this problem is known as envy-free cake-cutting, where fairness is defined as each person believing their piece is the best slice (or at least as good as everyone else's), effectively preventing envy altogether.
Now pause. Think about how to divide a cake for two people without causing envy?
The simplest envy-free method for two people is "Divide and Choose." One person cuts the cake into two pieces, which they feel are equal in value. The other person then chooses their favorite piece first. The Divide and Choose method works because both parties' best strategies inevitably lead to a fair cut.
The cutter will try to divide evenly because they know they'll get the leftover piece. The chooser will always pick the piece they prefer, so neither person envies the other.
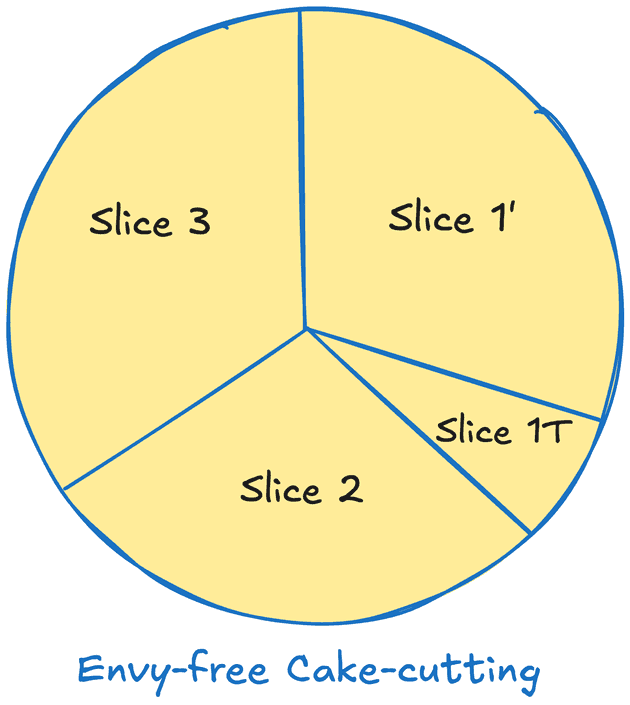
However, with three people, ensuring envy-freeness gets trickier. Mathematicians John Selfridge and John Conway independently discovered the Selfridge-Conway procedure. Here's how it works:
- Person A divides the cake into three equal slices (Slice 1, Slice 2, Slice 3).
- If Person B thinks all three slices are equal, then each player chooses a slice in this order: Person A, Person B, Person C. Problem solved.
- If Person B identifies the largest slice (said Slice 1), they then trim it slightly to be Slice 1' and match their second-choice slice (said Slice 2), setting aside the trimmings (called Slice 1T).
- Person C selects a slice first, then Person B chooses next (must take the trimmed piece Slice 1' if still available), leaving Person A with the last piece.
- Finally, if Person C picks Slice 1', Person B needs to divide Slice 1T into three. Then each player chooses a slice in this order: Person C, Person A, Person B. Problem solved. Vice versa, if Person B picks Slice 1'.
You can read an analysis of why the Selfridge-Conway procedure ensures envy-freeness here, and this method can even be generalized to N partners.
Moreover, envy-free cake-cutting is more than just a method for equitable division. Inspired by this, a common question raised in political science is whether it is truly necessary to get a third-party judge to ensure fairness in political conflicts.