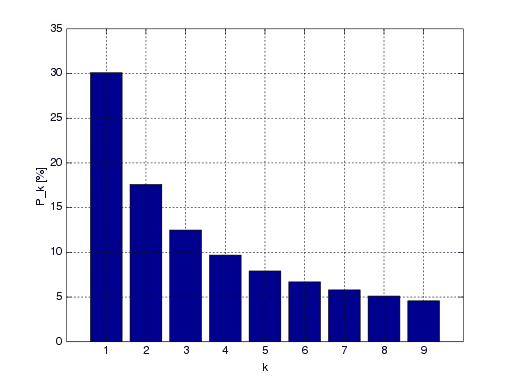
Benford's Law: The leading digit tends to be small for many real-life numerical data. The number 1 appears 30% of the time as the leading digit.
Article: Benford's Law
How to possibly detect fraud in an election just by analyzing the vote counts? We can get the distribution of the first digits of the vote counts and see whether number 1 appears more as the first digit.
Benford's Law, also known as the First-digit Law, described that the first digits of many real-life numerical data tend to follow an interesting distribution:
The distribution is not a uniform distribution nor a normal distribution. The number 1 appears about 30% of the time as the leading digit, and the number 2 appears about 17%. The leading digit tends to be small.
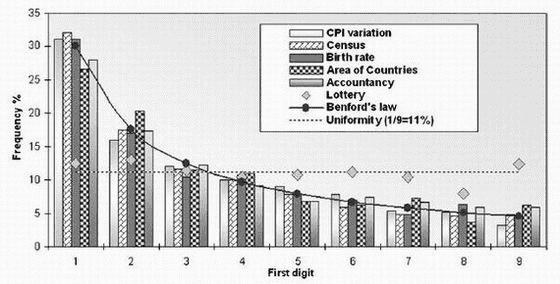
Benford's Law can be applied to many areas: the stock index history, the areas of countries, the length of the world's rivers, the numbers in newspapers' front-page headlines, etc. Below image from a physics journal shows that Benford's Law is applicable to various datasets, including CPI variation, Census, Birth rate, Area of countries, Lottery numbers, etc.
In fact, Benford's Law tends to be more accurate when the data are distributed across multiple orders of magnitude, and it is most accurate when the data are distributed evenly across multiple orders of magnitude. For instance, we can expect that Benford's Law would apply to the populations of different regions in the US. But if we define the region as a town with a population between 100 and 999, Benford's Law may not hold.